Hack New Year: MD5 Chain com Rainbow Table
Antes de qualquer coisa, gostaria de desejar a todos um feliz ano novo cheio de felicidades e que seus objetivos sejam edificados em 2010.
Criptografia com certeza é um assunto de interesse de muitos, porém por ser uma área tão extensa e de pré-requisitos (álgebra, geometria, trigonometria, teoria dos números, etc) que realmente não agradam alguns muitas vezes não são estudadas como hobby.
A criptoanálise é o ramo da ciência que estuda métodos de criptografia, capacitando ao profissional fazer a análise de um algoritmo criptográfico quanto a sua complexidade, podendo definir um algoritmo como forte (de difícil quebra) ou fraco (de fácil quebra).
Como dito, para se estudar criptografia, geralmente tem-se a necessidade de um forte embasamento matemático. Para se ter idéia, algumas linhas da matemática pura estudados a 20 anos atrás são chave fundamental para os melhores algoritmos de criptografia da atualidade.
Alguns ramos de estudo de criptografia não necessitam de um embasamento profundo em matemática. Um desses ramos é o Hash Chain, base para o tão conhecido Rainbow Table (vide Project RainbowCrack), que utiliza uma técnica chamada Time-memory Tradeoff (TMTO).
Em um ataque de força-bruta (brute-force) convencional a um algoritmo de hash, são gerados todas as possíveis senhas com seus respectivos hashes, e então procura-se um determinado hash para tentar obter a senha original. Porém, levando em consideração uma senha composto das letras de a à z (26 letras) e uma senha de até 7 caracteres, temos o total de:
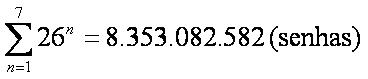
O maior problema não é calcular as senhas, e sim armazená-las, já que só para armazenar cada um dos 16 bytes do hash MD5 serão necessários mais que 124Gb de espaço. Se fosse até 8 (oito) caracteres esse valor iria mais que dobrar.
O Time-Memory Tradeoff tem por objetivo reduzir drasticamente a quantidade de memória utilizada em troca de um processamento um pouco maior, porém esse processamento poderia ser feito uma única vez e, dentro a tabela de hash bastaria apenas consultar.
Para se reduzir o tamanho do espaço armazenado, utiliza-se o chamado Hash Chain, que tem por finalidade armazenar uma palavra pertencente ao alfabeto e um hash não necessariamente equivalente a ela.
Iremos tomar como exemplo um alfabeto contendo as letras minúsculas de a à z. Com isto temos 26 letras em nosso alfabeto. Uma palavra é qualquer sequência de caracteres, todos pertencentes ao alfabeto dado e um dicionário é um conjunto de palavras.
O Hash Chain é formado da seguinte forma, dado uma palavra do dicionário, aplica-se uma função de hash H() e em seguida aplica-se uma função R(), tal que R() resulte em uma palavra também pertencente ao dicionário. Faz-se essa operação uma determinada quantidade de vezes (aqui chamadas de iterações) e, ao final, armazena-se o hash resultante, por exemplo:
H("aaaaaa") = 281DAF40
R(281DAF40) = "sgfnyd"
H("sgfnyd") = 920ECF10
Ou, em forma de cadeia:
aaaaaa —[H]→ 281DAF40 —[R]→ sgfnyd —[H]→ 920ECF10
No exemplo acima fizemos apenas duas iterações com a palavra aaaaaa. Inicialmente aplicamos a função de hash e obtivemos o valor 281DAF40. Em seguida foi aplicação a função R resultando na palavra sgfnyd , pertencente ao dicionário. Por ultimo aplicou-se novamente a função de hash resultando no hash 920ECF10.
Dado um hash para consultar, verifica-se se ele esta contido na tabela de hash’s gerada. Caso ele seja encontrado, é provável que a partir da palavra inicial consiga-se obter a palavra equivalente ao hash. Por exemplo, se tivermos o hash 920ECF10, podemos encontrá-lo na tabela, sendo equivalente a palavra inicial aaaaaa, bastando apenas fazer as operações H() e R() algumas vezes até encontramos a palavra que tenha o hash dado ou não encontrarmos (atingindo o máximo de iterações – muito azar). Caso o hash procurado não esteja na tabela, aplica-se consecutivamente as funções R() e H() no hash fornecido, procurando novamente na tabela, fazendo assim com que o hash fornecido converja à um hash da tabela ou atinja o número máximo de iterações (caso não seja encontrado).
É importante ressaltar que a função R() não pode ter qualquer aleatoriedade, ou seja, um valor de hash é sempre transformado na mesma palavra do dicionário. A diferença do Hash Chain puro para o Rainbow Table, é que o segundo possui diversas funções R que transformam um hash qualquer em uma palavra do dicionário, tentando assim evitar colisões (dois hash resultarem na mesma palavra).
Para efeitos de ilustração escrevi um código como prova de conceito (p0c), que gera em tempo real um dicionário, faz diversas iterações e depois procura um dado hash. É importante deixar claro que esse código é somente demonstrativo, porém ele pode futuramente virar um projeto da Hack N’ Roll.
Algumas limitações dele é o dicionário ser fixo (letras de a à z), e você tem que fornecer o tamanho da senha do hash (isso o torna completamente inútil sozinho em um ambiente real). Além disso, teria que melhorar (e muito) a função que transforma o hash em uma palavra do dicionário.
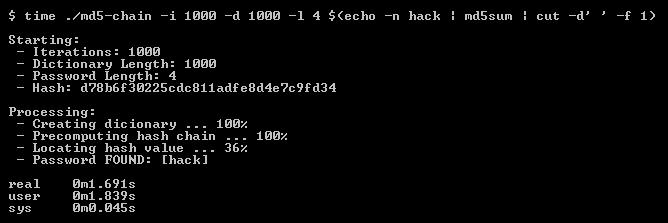
A ferramenta faz o que promete, porém algumas (muitas) vezes ele não encontra a palavra solicitada. Isso se dá porque o dicionário inicial é gerado aleatóriamente, para um melhor resultado, basta executar novamente com os mesmos parâmetros até ele encontrar a palavra solicitada:
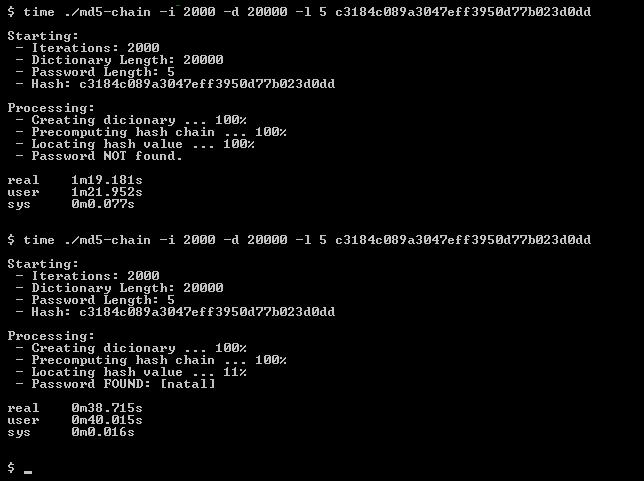
Não recomendo tentar utilizar o md5-chain como ferramente de quebra de hash MD5. Ele foi escrito com o único propósito de explicar o conceito de hash chain, time-memory tradeoff e como funciona o projeto RainbowCrack. Este ultimo já possui diversas melhorias matemáticas além de ter instruções específicas para trabalhar com GPU (processadores de placas de vídeo).
No projeto RainbowCrack, a tabela palavra/hash é gerada e armazenada em arquivo, sempre fazendo algumas verificações. Dessa forma bastaria fazer as consultas necessárias e obter os resultados.
O código-fonte do md5-chain pode ser obtido aqui. Sinta-se livre para modificá-lo e estudá-lo à vontade. Um desafio seria reescrever a função makepass() que gera uma palavra a partir de um hash, cuja execução com um dicionário inicial de 2000 palavras e 2000 iterações de uma senha de 5 caracteres não gere muitas (ou nenhuma) repetição.
Bom estudo e feliz hack’n roll.


